Introduction

I recently finished reading Reinforcement Learning: An Introduction by Sutton and Barto. Inspired by the book, I implemented the actor-critic algorithm and learned a lot. My first step was translating the pseudocode outlined in the book into JAX. If you’re new to reinforcement learning, it’s better to start by implementing a solution to a multi-armed bandit problem and familiarize yourself with temporal difference learning as these are foundational concepts.

Reinforcement Learning

Reinforcement learning is a class of algorithms designed to train a model, called a policy, to take actions that maximize the total reward received over time. It is called reinforcement learning because rewards reinforce behaviors that lead to higher rewards.

These algorithms require functional approximation, with deep learning being a particularly promising approach.

Actor Critics

Actor-critics are a class of reinforcement learning algorithms that use two models to teach each other. Both the actor and the critic observe the environment as input but produce different outputs.

• The actor outputs an action distribution from which an action can be sampled.
• The critic outputs a prediction of the total reward remaining in the episode or the future reward rate.

The critic’s predictions always depend on the current policy; a better policy generally leads to more rewards. Thus, when the actor improves, the critic needs to be updated to match the enhanced performance of the new actor.

The actor model can use the critic’s value estimations to adjust the action distribution towards actions that lead to better reward predictions.

In this way, the actor and critic balance, continually adjusting towards a better policy.

Implementation

I started with the pseudocode for a one-step actor-critic from Sutton and Barto. I recommend reading this book yourself, but I’ll do my best to translate the notation into an intuitive explanation.

One-step Actor-Critic (episodic), for estimating $\pi_\theta\approx\pi_*$

Input: a differentiable policy parameterization $\pi(a|s,\boldsymbol{\theta})$
Input: a differentiable state-value function parameterization $\hat{\upsilon}(s,\bold{w})$
Parameters: step sizes $\alpha^\theta > 0, \alpha^w > 0$
Initialize policy parameter $\bold{\theta}\in\R^{d'}$ and state-value weights $\bold{w}\in\R^d$ (e.g., to 0)
Loop forever (for each episode):
   Initialize $S$ (first state of the episode):
   $\textit{I} \leftarrow 1$
   Loop while $S$ is not terminal (for each time step):
       $A \backsim \pi (\sdot|S,\boldsymbol{\theta})$
       Take action $A$, observe $S'$, $R$
       $\delta \leftarrow R + \gamma \hat{\upsilon}(S', \bold{w}) - \hat{\upsilon}(S, \bold{w})$
       $\bold{w} \leftarrow \bold{w} + \alpha^\bold{w} \delta \nabla \hat\upsilon (S,\bold{w})$
       $\boldsymbol{\theta} \leftarrow \boldsymbol{\theta} + \alpha^{\boldsymbol{\theta}}I\nabla \ln \pi(A|S,\boldsymbol{\theta})$
       $I \leftarrow \gamma I$
       $S \leftarrow S'$

Algorithm outline taken from: Sutton, R. S., & Barto, A. G. (2018). Reinforcement Learning (2nd ed.). MIT Press.

Some notes on the above:

• Variables
  • $S$ is the observation from the environment or “state” this is the input for both the actor and critic about the environment during the current time step
  • $\gamma$ is the discount, this is used to value long term rewards less than immediate rewards.
  • $I$ stands for the importance, it starts at 1.0 but diminishes with the discount over the course of the episode. We use it to scale the actor learning rate down the more the episode has progressed.
• Functions
  • $\pi (\sdot|S,\boldsymbol{\theta})$ this is a function that samples a random action out of the action distribution
  • $\pi(A|S,\boldsymbol{\theta})$ this gives of the likelihood a given action would be selected under the current policy
  • $\hat{\upsilon}(S, \bold{w})$ this is the estimate of the cumulative discounted reward starting at S

Data Structures

class TrainingState(NamedTuple):
    importance: ArrayLike
    actor_params: Any
    critic_params: Any


class UpdateArgs(NamedTuple):
    discount: float
    actor_learning_rate: float
    critic_learning_rate: float

    obs: ArrayLike
    action: ArrayLike
    reward: ArrayLike
    next_obs: ArrayLike
    done: ArrayLike

Sample an action

$\pi (\sdot|S,\boldsymbol{\theta})$

We need a way to select actions from our policy. The solution depends on whether the actions for the environment are continuous or discrete. For this tutorial, we assume our action will always be one from a set of discrete actions.

A common way to handle this is to interpret the outputs of the actor model as logits for each possible action. Luckily, NumPy (and JAX) has a built-in function for picking a random action from a set of logits.

@partial(jax.jit, static_argnums=0)
def sample_action(actor_model, training_state, obs, rng_key):
    logits = actor_model.apply(training_state.actor_params, obs)
    return random.categorical(rng_key, logits)

Update our parameters

Calculating the TD error

$\delta \leftarrow R + \gamma \hat{\upsilon}(S', \bold{w}) - \hat{\upsilon}(S, \bold{w})$

If our value function $\hat{\upsilon}(S, \bold{w})$ is an estimate of the total reward left to receive at observation S, then $\hat{\upsilon}(S, \bold{w}) - \hat{\upsilon}(S+n, \bold{w})$ should be an estimate of the reward received between S and S+n. If n is 1, meaning it’s the following observation, then this difference should be an estimate of the instantaneous reward at S. The difference between the estimated reward and the actual instantaneous reward is the temporal difference error $\delta$.

If the observation is the episode terminal (done = True), no further rewards are possible, so the state value should always be 0.

This TD error will be used to update both our critic to make better estimates and our actor to take actions that lead to more rewards.

def temporal_difference_error(critic_model, critic_params, update_args):
    state_value = critic_model.apply(critic_params, update_args.obs)
    next_state_value = jax.lax.cond(
        update_args.done,
        lambda: 0.0,
        lambda: update_args.discount
        * critic_model.apply(critic_params, update_args.next_obs),
    )

    estimated_reward = state_value - next_state_value
    td_error = update_args.reward - estimated_reward

    return td_error

Updating the critic

$\bold{w} \leftarrow \bold{w} + \alpha^\bold{w} \delta \nabla \hat\upsilon (S,\bold{w})$

The temporal difference error can improve the critic predictions by moving in the direction of the gradient at S, scaled by the TD error. Value(S+1) + reward is a better prediction than Value(S), and our TD error already represents this difference. If we simply move a step in the direction of the gradient of the value at S, multiplied by the TD error, our value estimations should improve.

This also provides a way for our later state predictions to influence our earlier state predictions, so that with enough repetitions, the predictions at the end of the episode should help determine the predictions at the beginning of the episode.

This is technically semi-gradient descent because the gradient at Value(S+1) is ignored. A consequence is that the value function doesn’t converge to the actual reward approximation, but a point close to it called TD fixed point.

def update_params(params, grad, step_size):
    return jax.tree_map(
        lambda param, grad_param: param + step_size * grad_param,
        params, grad
    )


def update_critic(critic_model, critic_params, update_args, td_error):
    critic_gradient = jax.grad(critic_model.apply)(critic_params, update_args.obs)
    critic_params = update_params(
        critic_params,
        critic_gradient,
        update_args.critic_learning_rate * td_error,
    )

    return critic_params

Updating the actor

$\boldsymbol{\theta} \leftarrow \boldsymbol{\theta} + \alpha^{\boldsymbol{\theta}}I\nabla \ln \pi(A|S,\boldsymbol{\theta})$

We can also use the TD error to select better actions. The basic idea is that if the reward exceeds our expected reward for the state before the action was taken, we should increase the odds that that action will be retaken in a similar state. Conversely, if the reward is less than the expected reward, we should decrease the odds that the action is taken.

The intuition behind this is if the value function is the average reward received for the actions selected by the current policy for that state. We are increasing the likelihood that better-than-average actions are taken and decreasing the likelihood that worse-than-average actions are taken.

We use the log of the action probability in the gradient because if the action is already highly likely to be selected, we want to adjust it less.

def action_log_probability(actor_model, actor_params, obs, action):
    logits = actor_model.apply(actor_params, obs)
    return nn.log_softmax(logits)[action]


def update_actor(actor_model, actor_params, update_args, td_error, importance):
    actor_gradient = jax.grad(action_log_probability, argnums=1)(
        actor_model, actor_params, update_args.obs, update_args.action
    )
    actor_params = update_params(
        actor_params,
        actor_gradient,
        update_args.actor_learning_rate * td_error * importance,
    )

    return actor_params

Combined Update Function

@partial(jax.jit, static_argnums=(0, 1))
def update_models(
    actor_model,
    critic_model,
    training_state: TrainingState,
    update_args: UpdateArgs,
) -> TrainingState:
    actor_params = training_state.actor_params
    critic_params = training_state.critic_params
    importance = training_state.importance

    td_error = temporal_difference_error(critic_model, critic_params, update_args)
    critic_params = update_critic(critic_model, critic_params, update_args, td_error)
    actor_params = update_actor(
        actor_model, actor_params, update_args, td_error, importance
    )

    importance = jax.lax.cond(
        update_args.done, lambda: 1.0, lambda: importance * update_args.discount
    )

    return TrainingState(
        importance=importance, actor_params=actor_params, critic_params=critic_params
    )

Training loop

Now we can bring it all together with a complete training loop with the gymnasium library (you can also use Gymnax to run your environment on the gpu along with your training code)

Training loop with gym

obs, _ = env.reset()
for step in range(total_steps):
    rng_key, action_key = random.split(rng_key)
    action = actor_critic.sample_action(actor_model, training_state, obs, action_key)

    next_obs, reward, terminated, truncated, _ = env.step(action.item())
    done = terminated or truncated

    update_args = actor_critic.UpdateArgs(
        actor_learning_rate=actor_learning_rate(step),
        critic_learning_rate=critic_learning_rate(step),
        discount=discount,
        obs=obs,
        action=action,
        reward=reward,
        next_obs=next_obs,
        done=done,
    )

    training_state = actor_critic.update_models(actor_model, critic_model, training_state, update_args)
    obs = next_obs

    total_reward += reward

    if done:
        obs, _ = env.reset()

For a full example of the code, see: https://github.com/gabe00122/tutorial_actor_critic/tree/main/tutorial_actor_critic/part1

Results

Here are the hyper parameters I used for training on gym cart-pole, 500 is the max score.

total_steps = 800_000
actor_learning_rate=linear_schedule(0.0001, 0.0, total_steps)
critic_learning_rate=linear_schedule(0.0005, 0.0, total_steps)
discount=0.99
actor_features = (64, 64)
critic_features = (64, 64)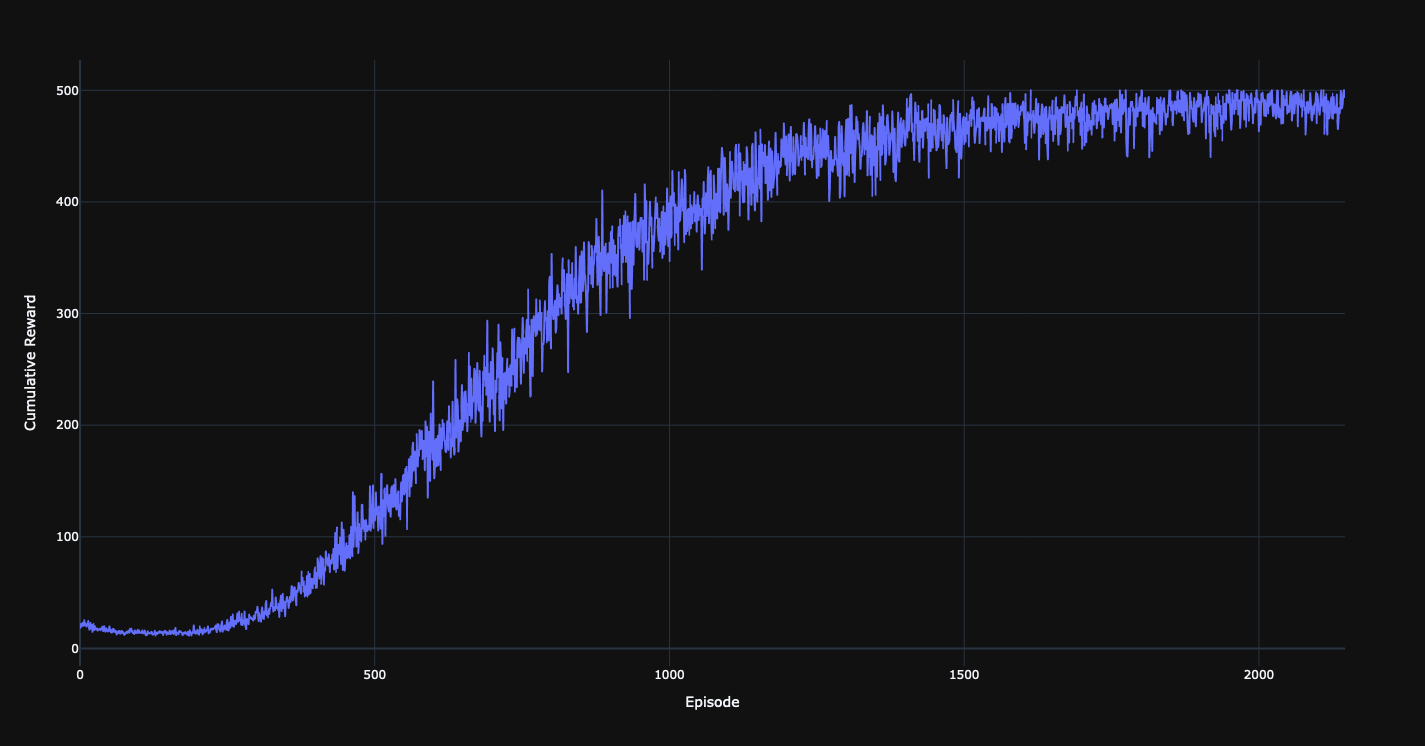

Next Steps

This is only a basic implementation of an actor-critic algorithm. While this basic implementation is effective for environments like CartPole, the actor-critic algorithm is a versatile tool that, with the right techniques and improvements, can be harnessed to handle a wide range of complex problems. Here are just a few examples of possible improvements:

• Reframe the Update as a Loss Function: Use calculus to reframe the algorithm’s update as a loss function. This approach simplifies employing optimizers like Adam and using training batches.
• Train with batches Having more data in a training batch can help stabilize training and more effectively use parallelism; a common strategy is using a replay buffer. Alternatively, vectorized environment training can also be used, but it’s not uncommon to see both strategies employed together
• Regularization Techniques Techniques, such as entropy or L2 regularization, may be helpful for reinforcement learning. Regularization can influence both exploration and sometimes prevent plasticity loss.
• Use More Steps The algorithm in this post only describes single-step actor critics. Multi-step approaches are well studied and can speed up training, but this comes at the cost of introducing more bias and making the TD fixed point farther from the true optima.
• Account for off-policy data This algorithm with only work for on policy training data, this is a serious limitation since data not generated with the current policy shouldn’t be used for training. Techniques such as importance sampling can help account for off policy data.

Using an Adam optimizer and vectorized training environments with some entropy regularization, I used this algorithm to learn tic-tac-toe, as can be seen in this demo